Basic Reverse Engineering (writeup) - Part 0x02

Introduction

---

I’ve started a course on Modern Binary Exploitation and throughout this course there are challenges and labs with which to practice exploitation techniques. It starts with an introduction to reverse engineering and I’ve decided to write about how I solved the challenges and take notes of the things I learned.

This (as you can see) is the third post and it will focus on the cmubomb challenge from the “Extended Reverse Engineering” class.

If you plan to take the course I highly encourage you not to read any further and try to solve the challenges yourself. You’ll learn much more that way.

For some of the challenges you don’t need to look at every assembly instruction but just looking at the function calls and byte/string comparisons you can immediately understand what input is expected without reversing the whole thing.

cmubomb

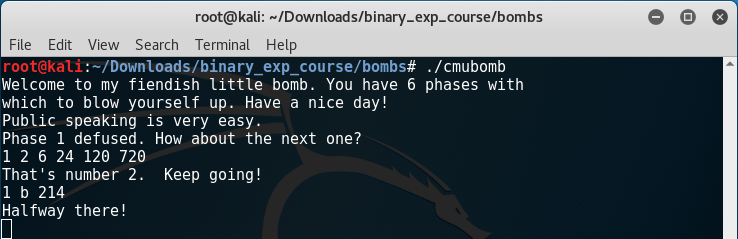
Starting the executable we’re presented with the following text:

When we open the executable with IDA, there is a function called phase1. And when you open it in graph view the answer is obvious.

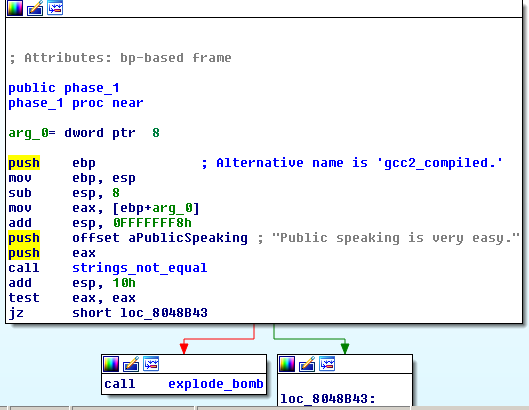
We enter ‘Public speaking is very easy.’ aaaaand…

Success!!

Phase 2

phase2:

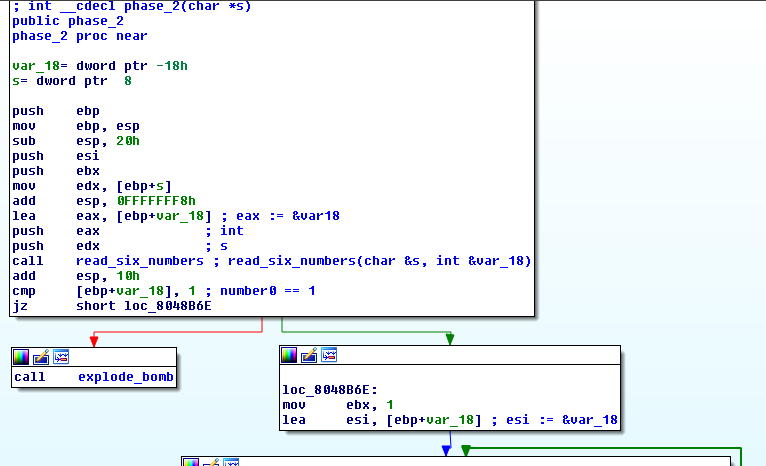
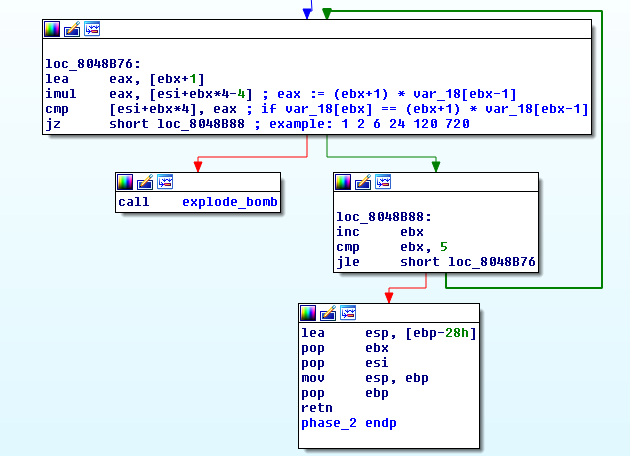
read_six_numbers:

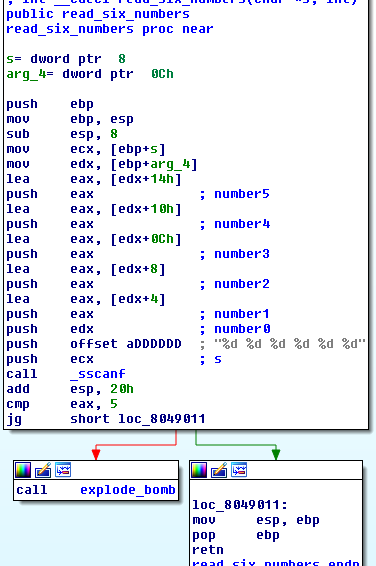
As you can see phase2:

• reads 6 numbers
• stores them in the integer array var_18
• expects that each number is (i+1) times bigger than the previous

For example:
var_18[1] should be equal to 2 x var_18[0]
var_18[2] should be equal to 3 x var_18[1]
and so on.

I chose to try 1 2 6 24 120 720

Phase 3

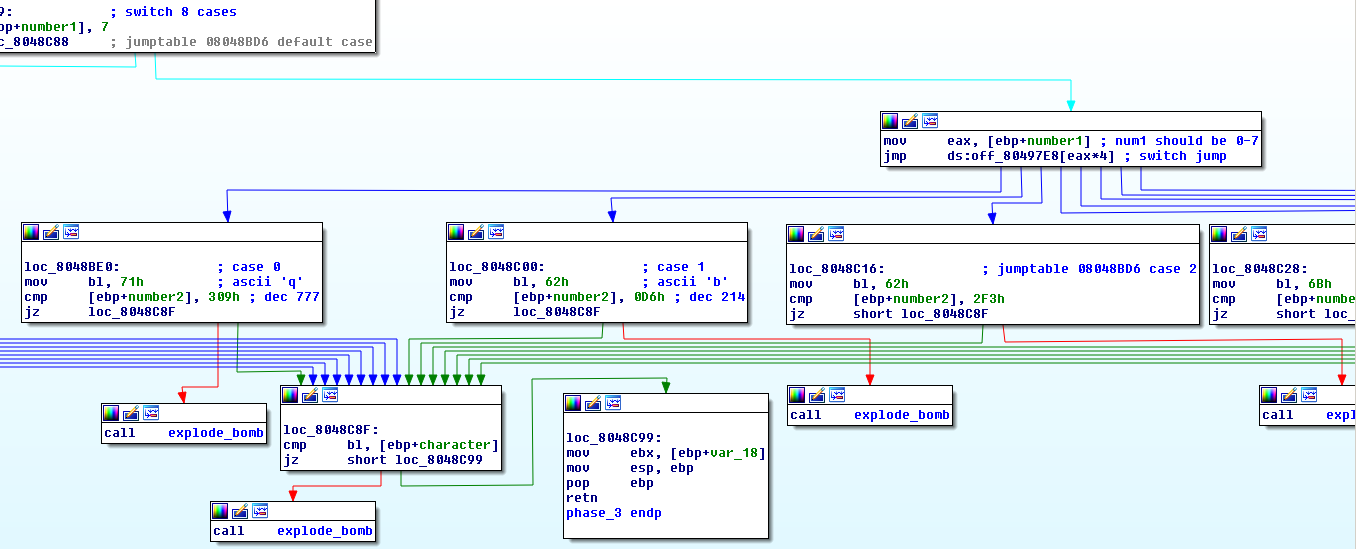
At phase 3 the expected input is a number, a character and again a number.
Next we enter a switch statement with 8 cases (0-7) and the first number of our input selects the case.

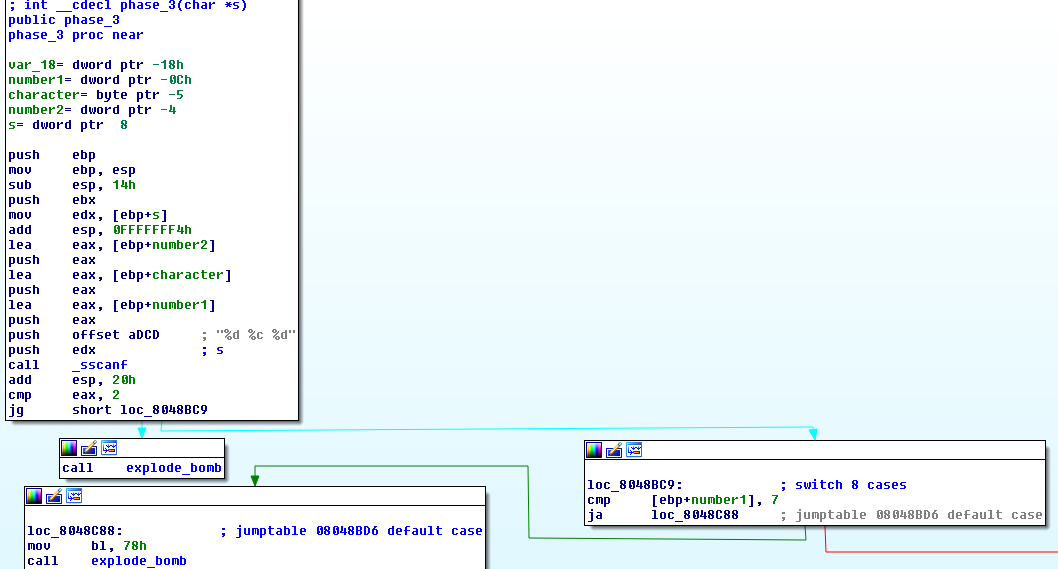
The case determines what character and second number should be expected form our input.
For case 1 that’s character 'b' and number2 = 214

Phase 4

phase4:

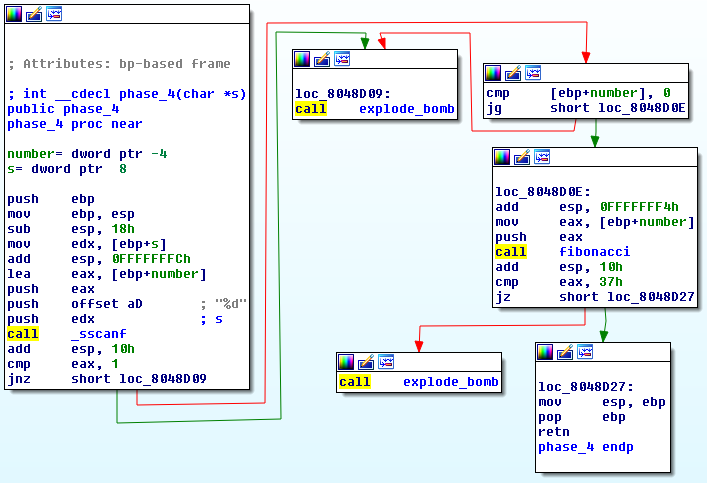
Phase 4 accepts one number as input and passes that number as an argument to a function, that I renamed to 'fibonacci'. Then it compares the result that the function returns with 0x37 (55 in decimal).

fibonacci:

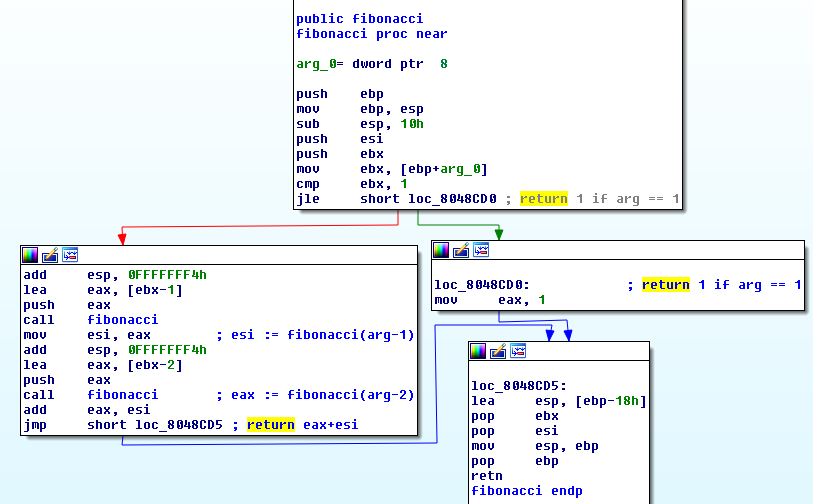
As you can see the function calls itself, so it’s a recursive function. It returns 1 if the argument is <= 1.
If the argument is 2 it returns fibonacci(2-1) + fibonacci(2-2) which would return ``.
If the argument is 3 it returns fibonacci(3-1) + fibonacci(3-1) which is 2 + 1 = 3.
If the argument is 4 it returns fibonacci(4-1) + fibonacci(4-2) which is 3 + 2 = 5.
And so on.

I think you see why I renamed the function fibonacci. It returns the n-th fibonacci number.
So which input would produce a result of 55?

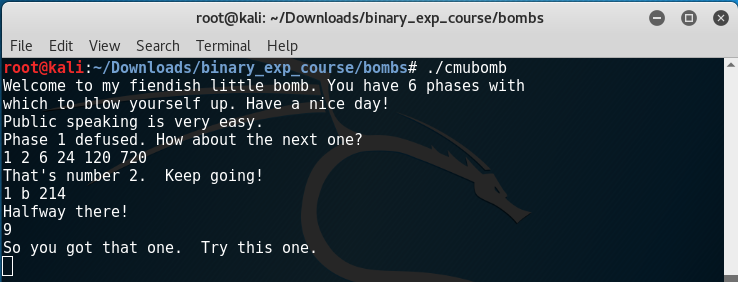
Phase 5

phase5:

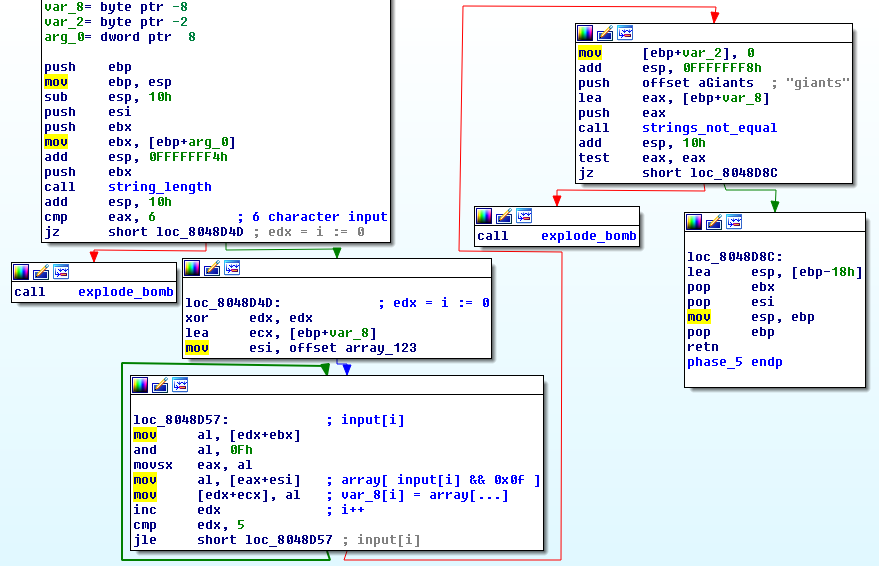
• Our input is stored in arg_0
• Accepts a 6 character input
• Uses edx as an iterator i
• Iterates through every element of our input , input[i]
• esi points to the character array array_123
• var_8 is an empty array
• The element at position[ input[i] && 0x0f ] of array_123 is stored in the i-th position of var_8
• var_8[i] = array_123[ input[i] && 0x0f ]
• Finally compares var_8 with the string "giants"

contents of array_123:

So we must enter such input, that it’s decoded by the algorithm to "giants". The AND operation, unlike XOR or NOT, is non inversible. That’s why we can’t just recreate the algorithm in reverse to see which string corresponds to "giants".

I wrote a bruteforce script that tries every 6 character combination of ascii printable characters.

#!/usr/bin/env python3

array_123 = 'isrveawhobpnutfg'
secret = 'giants'

output = []
for i in range(6):
   # find the index of secret[i] character 
   # in array_123      
   index = array_123.find( secret[i] )

   # try all ascii printable characters
   # with which the algorithm returns the
   # correct index
   for byte in range(33,127):
      if (byte & 0x0f) == index:
         b = chr(byte)
         output.append(b)
         # use only the first found character
         break

print(''.join(output))

$ ./phase5.py 
/0%+-!

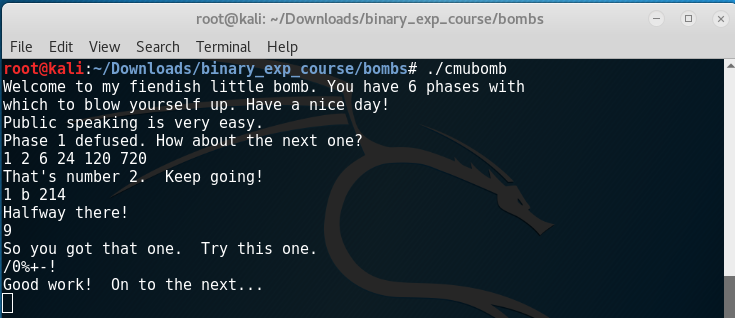
Phase 6

Phase 6 is harder then the previous phases. Let’s see the disassembly:

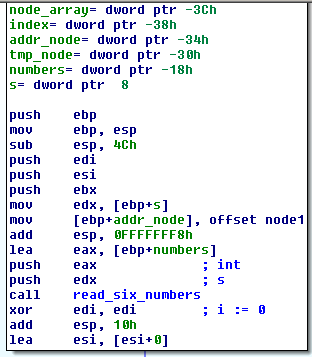
I’ve already renamed the variables and the arguments, but if you got this far it shouldn’t be a problem to find out their purpose yourself.

As you can see the function read_six_numbers is used again and then edi is prepared to be used as an loop iterator and initialized to zero. The numbers are save in the integer array numbers.

But before I continue, let’s see what is this mysterious node1.

It looks like a structure. There are other nodes as well. Hmm.. Let’s check it in gdb (pwndbg).

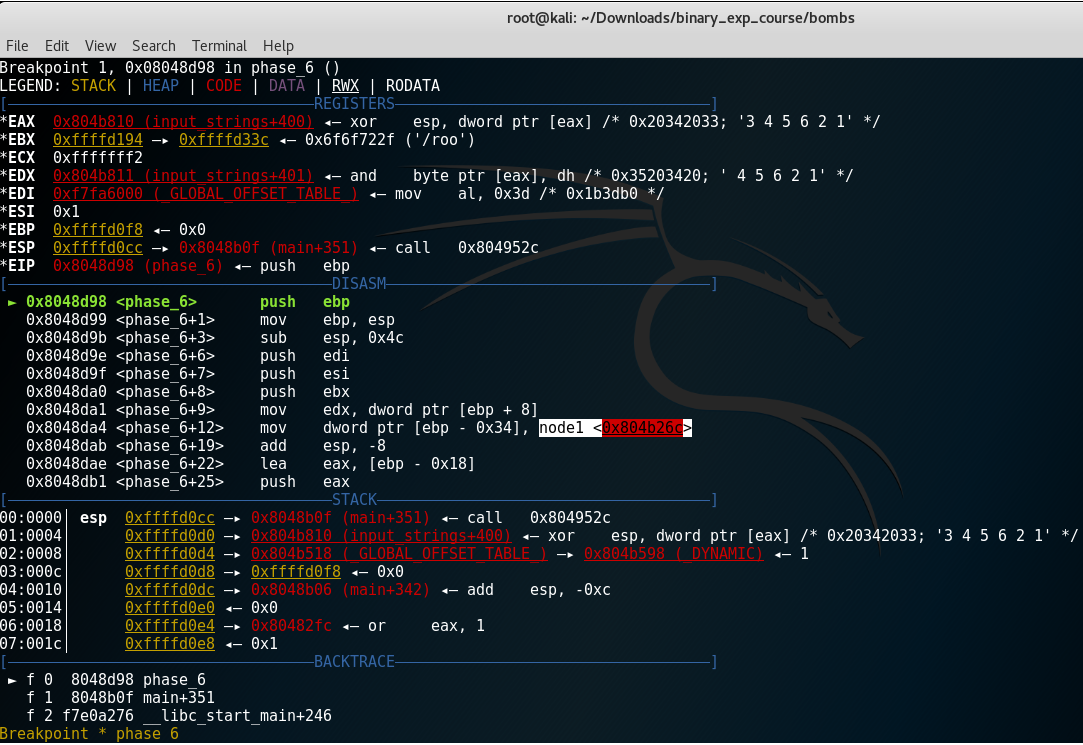
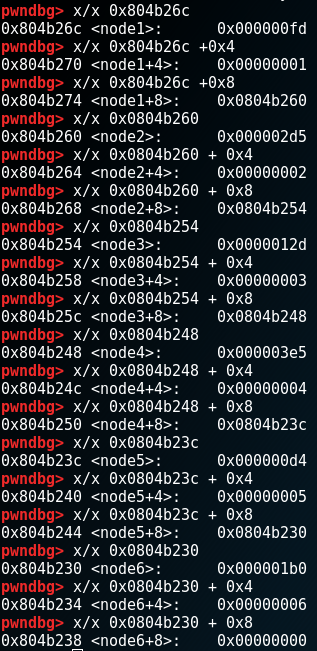
It’s a linked list of 6 structures. Node6 is the last one and points to null address. The structure looks something like this:

struct node{  // example address 0x804b26c
   int value;       // address 0x804b26c + 0x0
   int id;          // address 0x804b26c + 0x4
   char* next_node; // address 0x804b26c + 0x8
}

OK, continuing with the disassembly…

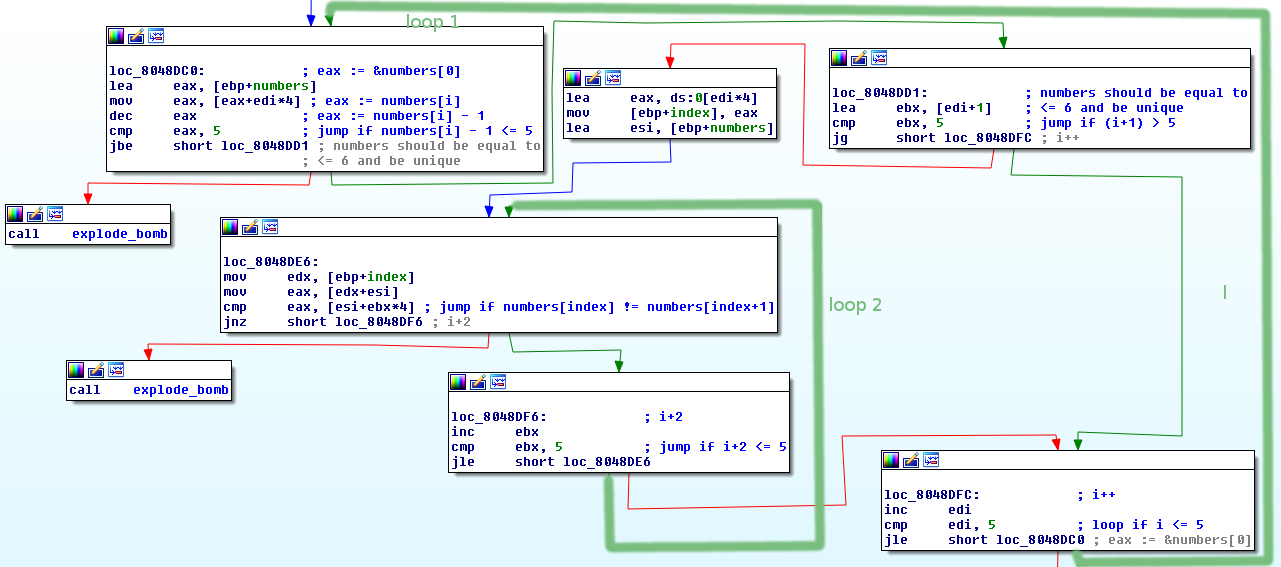
This part of the phase contains two loops.

• In the first (outer) loop each of our numbers is checked if it’s <= 6 (numbers[i] -1 <= 5)
• The second (inner) loop checks if the current number is equal to another number in the array. If it is the bomb blows.

This means that the expected input is 6 unique numbers with values <= 6. That is 1,2,3,4,5,6 but in any order.

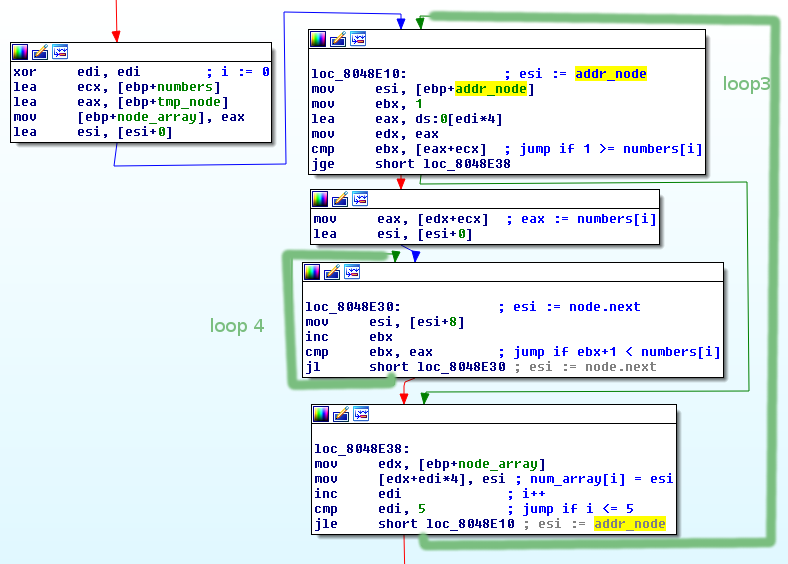
Again we have two loops.

• The outer loop (loop 3) iterates through our numbers[i]
• If numbers[i] is <= 1, then skip the inner loop
• addr_node was pointing to node1 (the beginning of the linked list)

• The current node is added as the i-th element to node_array[i]

• If numbers[i] > 1, then go to the inner loop (loop 4)
• (ebx start with value of 1) Iterate until ebx+1 = numbers[i]
• Set esi to node.next
• The result is that we get numbers[i]-th node of the list
• The second loop completes and the numbers[i]-th node is added as the i-th element of node_array[i]

So if our input is 2,1,4,3,6,5 node_array is going to be [node2, node1, node4, node3, node6, node5]

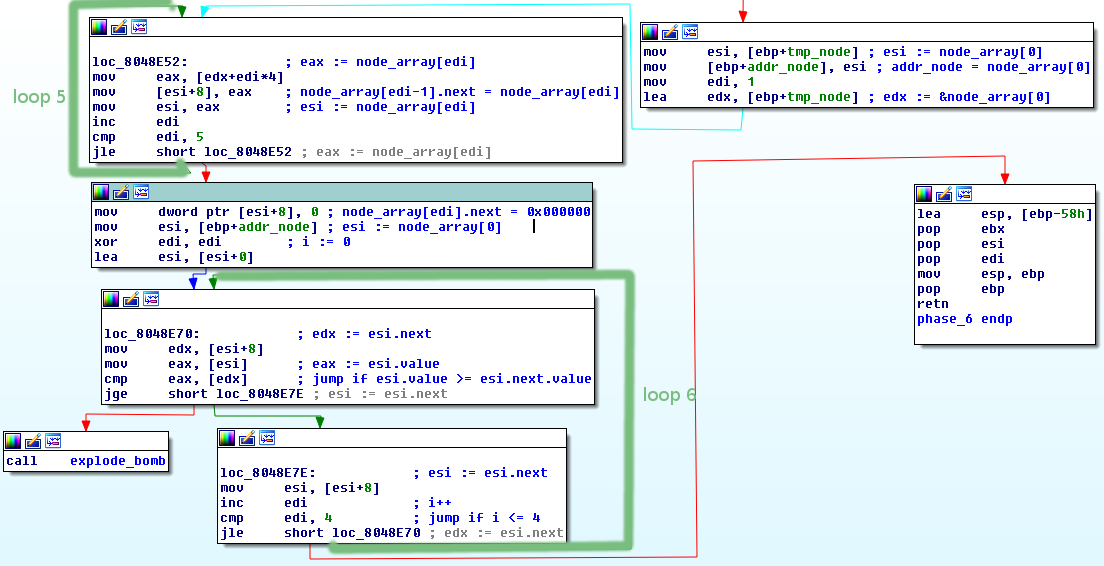
• The first loop iterates through node_array
• Sets the current node to point to the node thats next in the array
• i=1; node_array[i-1].next = node_array[i]
• After the loop last node is set to point to null address

If I use my previous example, the current linked list will be:
node2 -> node1 -> node4 -> node3 -> node6 -> node5 -> null

• The second loop goes through our new linked list
• Checks that the nodes are in such order, that their values are descending.
• current_node.value >= current_node.next.value

And the script that bruteforces the solution:

#!/usr/bin/env python3
import itertools

class node:
   def __init__(self, address, value, number):
      self.address = address
      self.value = value
      self.number = number
      self.next_node = None

   def set_next_node(self, next_node):
      self.next_node = next_node

def phase6( numbers ):

   node1 = node(0x0804b26c, 0x0fd, 0x1)
   node2 = node(0x0804b260, 0x2d5, 0x2)
   node3 = node(0x0804b254, 0x12d, 0x3)
   node4 = node(0x0804b248, 0x3e5, 0x4)
   node5 = node(0x0804b23c, 0x0d4, 0x5)
   node6 = node(0x0804b230, 0x1b0, 0x6)
   node_null = node(0x00000000, 0x0, 0x0)
   
   node1.set_next_node( node2 )
   node2.set_next_node( node3 )
   node3.set_next_node( node4 )
   node4.set_next_node( node5 )
   node5.set_next_node( node6 )
   node6.set_next_node( node_null )
   
   node_array = []   

   # numbers must be unique
   if len(numbers) != len( set(numbers) ):
      print('BOOM! Not unique!')
      return False

   # numbers must be between 1 and 6
   if max(numbers)-1 > 5:
      print('BOOM! Bigger than 6!')
      return False

   # create node_array based on the input numbers
   for i in range(6):
      nd = node1
      for j in range(1, numbers[i]):
         nd = nd.next_node
      node_array.append( nd )

   # set connections for the nodes in the node_array
   for i in range(1,6):
      node_array[i-1].set_next_node( node_array[i] )
   node_array[5].set_next_node( node_null )

   # values of nodes in node_array should be in descending order
   nd = node_array[0]
   for i in range(6):
      if nd.value < nd.next_node.value:
         #print('Boom! Not ascending!')
         return False
      #print('Value of node %d: %x' % (nd.number, nd.value))
      nd = nd.next_node
   
   return True

for n in itertools.permutations('123456', 6):
   numbers = []
   for i in range( len(n) ):
      numbers.append( int( n[i] ) )

   if ( phase6( numbers ) ):
      print('Valid key: ', numbers)
      input()

# ./phase6.py 
Valid key:  [4, 2, 6, 3, 1, 5]

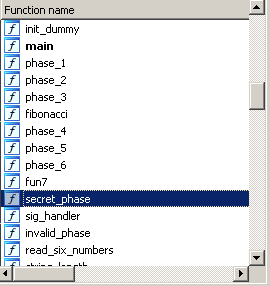
But wait! There’s more! If you look at list of function in IDA you’see that there is a secret phase:

Time to figure out how to access it.

THE SEARCH FOR THE SECRET PHASE

First, let’s check the cross references and see where that fucntion is called.

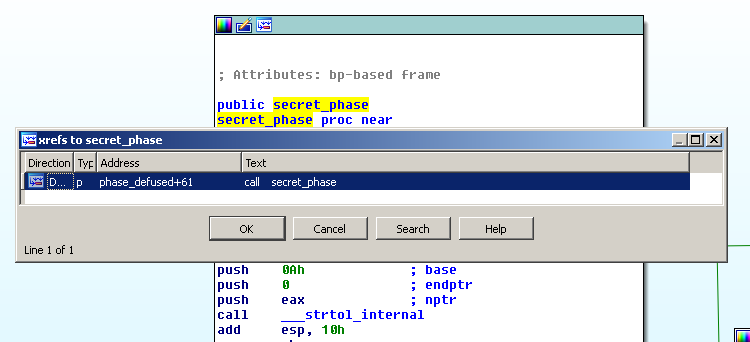
It gets called only from the function phase_defused. And phase_defused gets called in main.

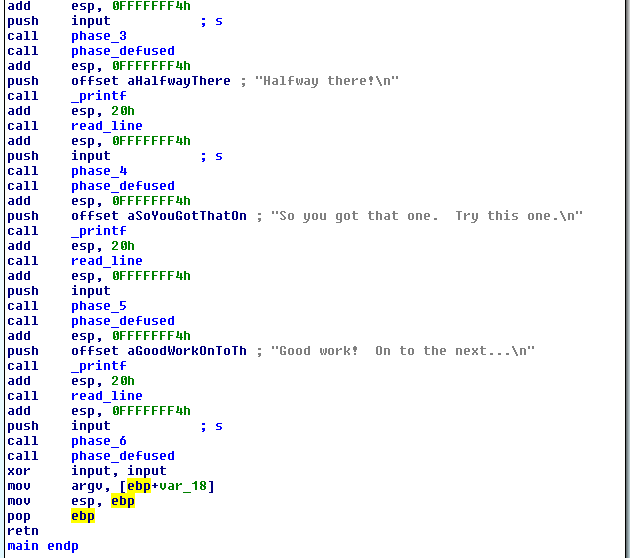
And not only it’s called in main, but it’s called right after each phase! And now we should look into phase_defused.

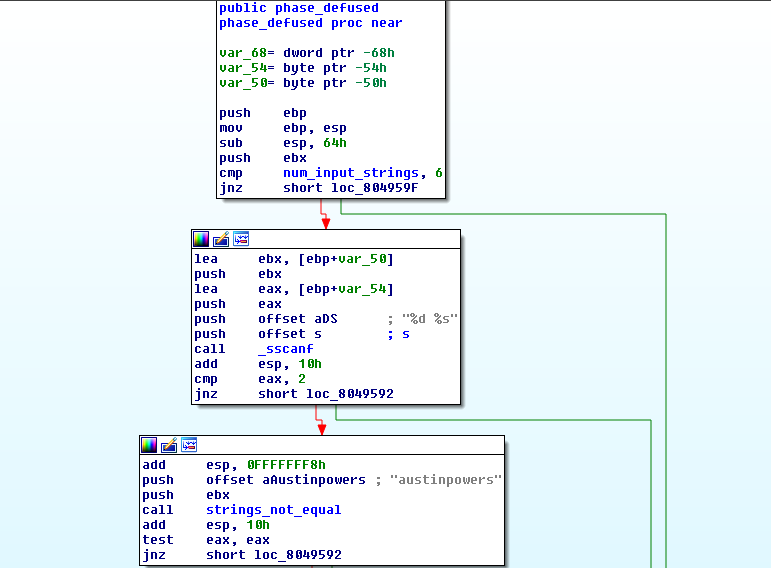
At the beginning it checks if num_input_strings == 6.
If it’s false then the function exits.
If it true, then it checks if the string s is in the form <integer> <string> as you can see from the sscanf call.

sscanf(s, "%d %s", &var_54, &var_50 )

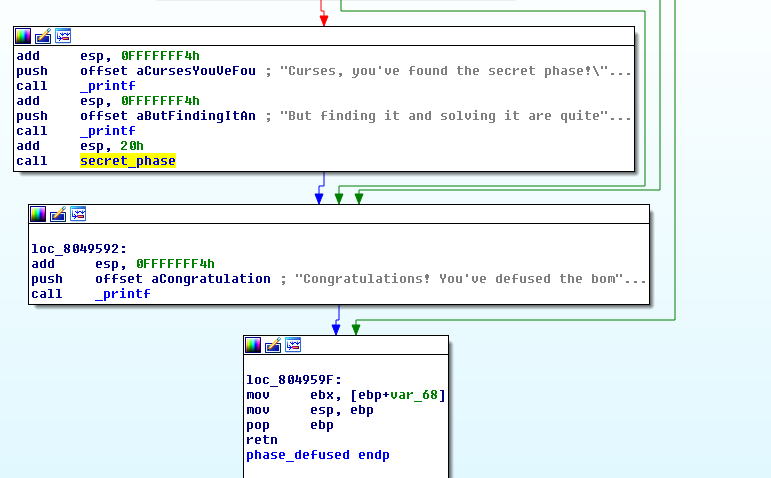
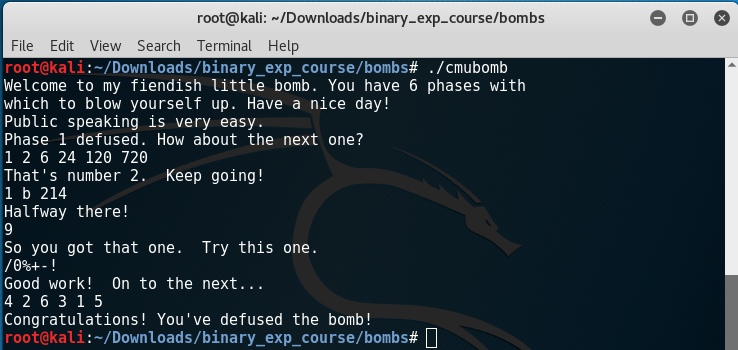
If it’s not -> outputs the message that we’ve defused the bomb (the one after completing phase 6). And if it is, it checks if var_50 is equal to "austinpowers". If true we enter the secret phase.

At first I thought that num_input_strings holds the number of strings in our current input. But then I started gdb (pwndbg) and noticed how the value changes.

pwndbg> run
Starting program: /root/Downloads/binary_exp_course/bombs/cmubomb 
Welcome to my fiendish little bomb. You have 6 phases with
which to blow yourself up. Have a nice day!
Public speaking is very easy.

Breakpoint * phase_1
pwndbg> info br
Num     Type           Disp Enb Address    What
1       breakpoint     keep y   0x08048b20 <phase_1>
   breakpoint already hit 1 time
2       breakpoint     keep y   0x08048b48 <phase_2>
3       breakpoint     keep y   0x08048b98 <phase_3>
4       breakpoint     keep y   0x08048d98 <phase_6>
pwndbg> print num_input_strings 
$2 = 1
pwndbg> conti
Continuing.
Phase 1 defused. How about the next one?
1 2 6 24 120 720

Breakpoint * phase_2
pwndbg> print num_input_strings 
$3 = 2
pwndbg> conti
Continuing.
That's number 2.  Keep going!
1 b 214

Breakpoint * phase_3
pwndbg> print num_input_strings 
$4 = 3
pwndbg> conti
Continuing.
Halfway there!
9
So you got that one.  Try this one.
/0%+-!
Good work!  On to the next...
4 2 6 3 1 5

Breakpoint * phase_6
pwndbg> print num_input_strings 
$5 = 6

num_input_strings, shows how many input strings have we typed, which is the same as telling us at which phase are we currently. It also makes sense that the string about bomb deactivation is printed after the check num_input_strings == 6.

Now I wanted to see how our input is read and stored. In the main function you can see that 'input' points the input that is passed to phase_x functions. But 'input' as you can see below is just the eax register.

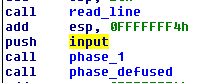
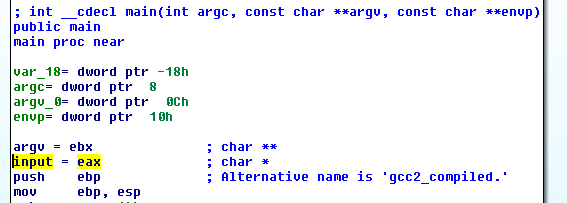
And what is the last thing that sets the eax register? The read_line function! At the beginning read_line calls skip function, I’ll show it first.

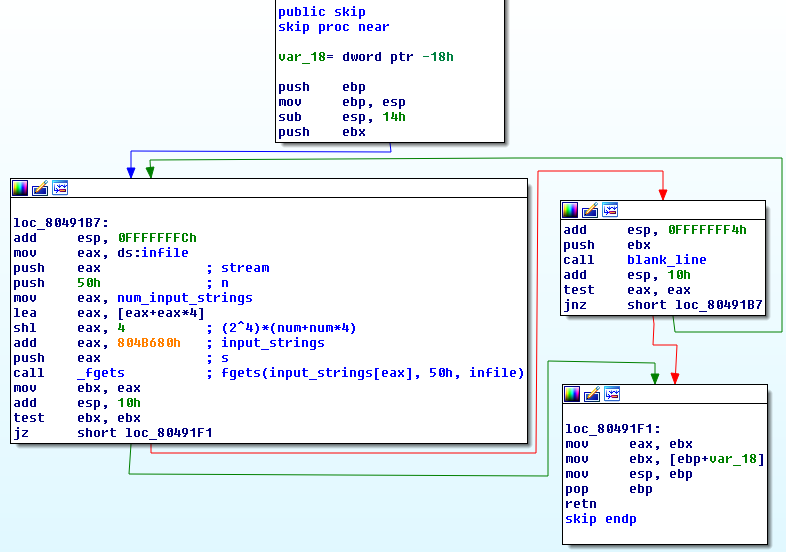
• input_strings is the buffer where all our input is stored.
• num_input_strings is how many times we had to type an input (starting value is 0)
• input_strings is split into 80 byte parts
• every time we write an input it’s saved in a different part of input_strings
• fgets is used to read 0x50 (decimal 80) bytes and save them in input_strings[eax]

num_input_strings = 0 (before phase_1) , 1 (before phase_2), 2 (before phase_3) ….

then

eax = (2^4) x (num_input_strings + num_input_strings x 4) will evaluate to = 0 , 80, 160, ….

then this is added to the address of input_strings which is equivalent to input_strings[eax] or input_strings[(2^4) x (num_input_strings + num_input_strings x 4)] or
input_strings[0]
input_strings[80]
input_strings[160]
….

And now the read_line function (I’ll show only the end):

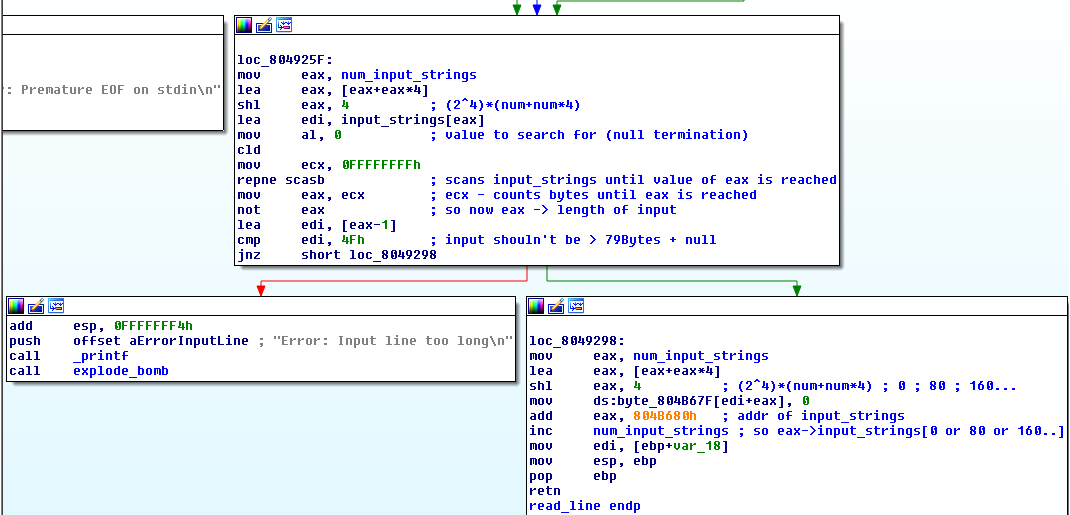
• Our input is checked if it is longer than 80 bytes
• eax is set to point to our input
• num_input_strings is incremented
• the function returns

I need to see where in input_strings, phase_defused expects the input for the secret phase to be, because I tried and it doesn’t work with phase6 ("4 2 6 3 1 5 austinpowers"). I used gdb for that. I set a breakpoint at phase_defused and after the phase_6 stage.

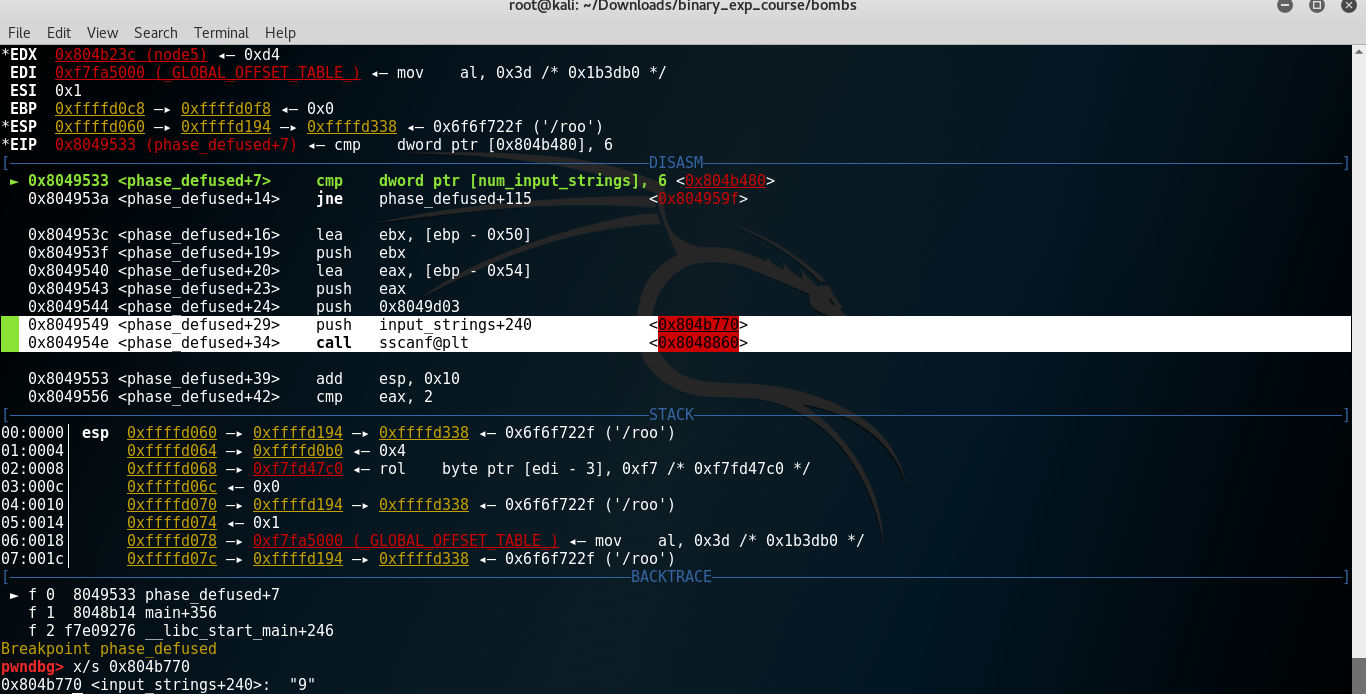
You can see that sscanf expects the input buffer to be at input_strings with an offset of 240 bytes. And right now the string that is saved there is "9". This was the answer for phase 4. So at phase 4 we need to type "9 austinpowers"!

Although phase 4 accepts only one number as input, this works because sscanf reads only the first strings that match the format specifiers and ignores everything after that.

sscanf("1 2 this is a string", "%d %d", &num1, &num2);
// will save 1 and 2 at num1 and num2 respectively and ignore the rest "this is a string"

That means the buffer input_strings contains "9 austinpowers", but phase 4 reads only the "9" and after phase 6, phase_defused will read both.

sscanf("9 austinpowers", "%d %s", &var_54, &var_50 )

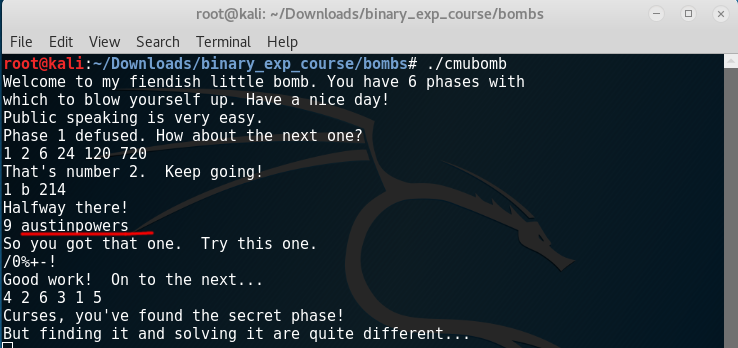
SECRET PHASE

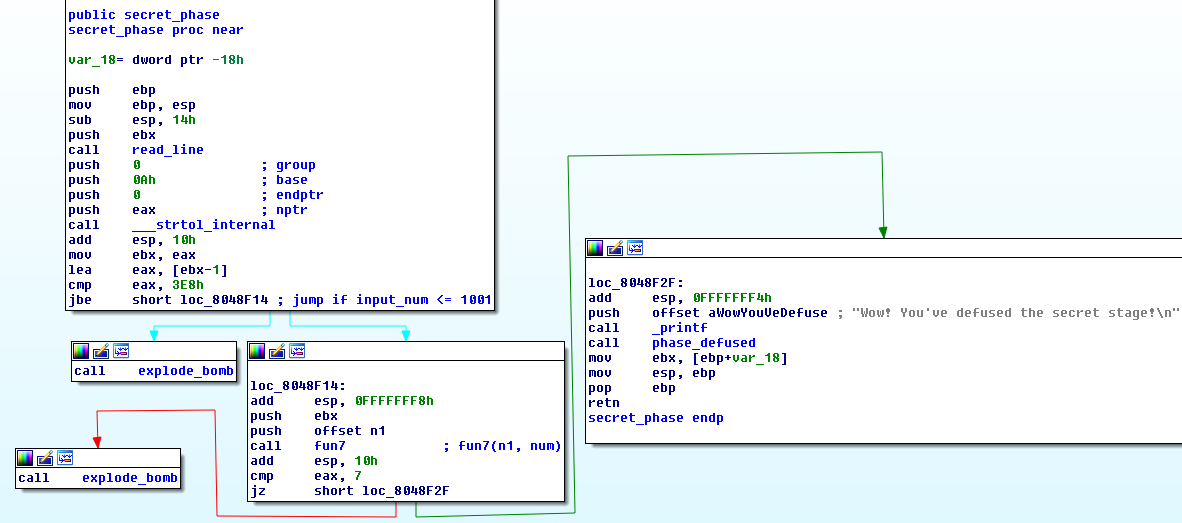
• First calls read_line function.
• Then call strtol (converts string to integer “9” -> 9) which means it accepts number as input.
• The input should be <= 1001
• Then calls the function fun7(n1, num), where num is our number
• The result from the function should be 7

Now let’s see what that n1 is.

It definitely looks like a structure again…

pwndbg> x/x 0x0804b320
0x804b320 <n1>:   0x00000024
pwndbg> x/x 0x0804b320 + 0x4
0x804b324 <n1+4>: 0x0804b314
pwndbg> x/x 0x0804b320 + 0x8
0x804b328 <n1+8>: 0x0804b308
pwndbg> x/x 0x0804b320 + 0xc
0x804b32c:  0x00000000
pwndbg> x/x 0x0804b314
0x804b314 <n21>:  0x00000008
pwndbg> x/x 0x0804b314 + 4
0x804b318 <n21+4>:   0x0804b2e4
pwndbg> x/x 0x0804b314 + 8
0x804b31c <n21+8>:   0x0804b2fc
pwndbg> x/x 0x0804b314 + 12
0x804b320 <n1>:   0x00000024

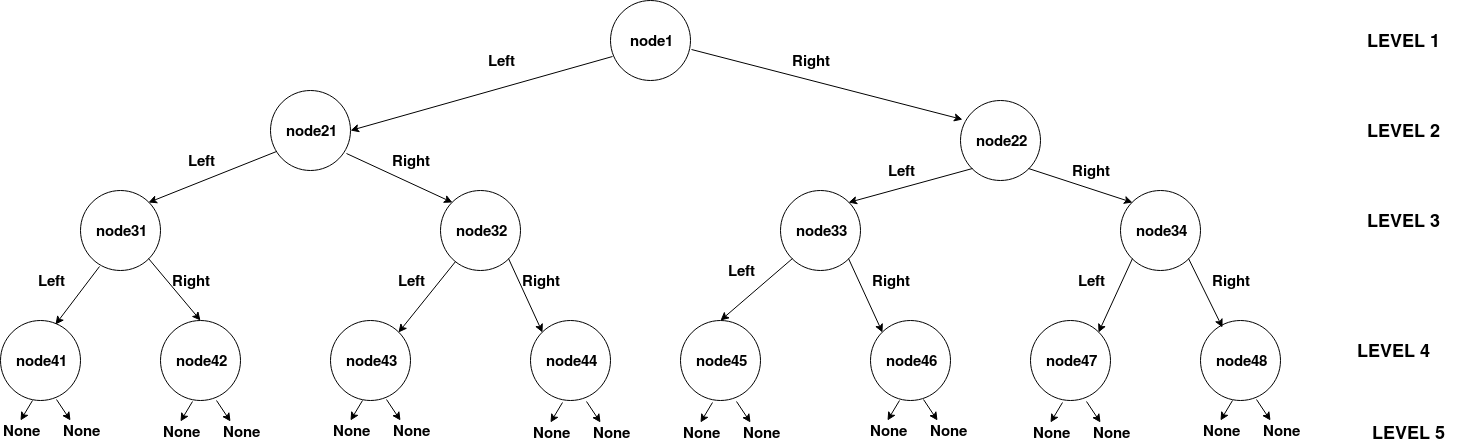
And again it looks like a linked list.
The structure looks like:

struct nn{ // example address 0x0804b320
   int value;     // 0x0804b320 
   char* next_left;    //0x0804b320 + 0x4
   char* next_right;   //0x0804b320 + 0x8
}

I traced all nodes so here’s a visual representation of the list/graph:

And the fun7 disassembly:

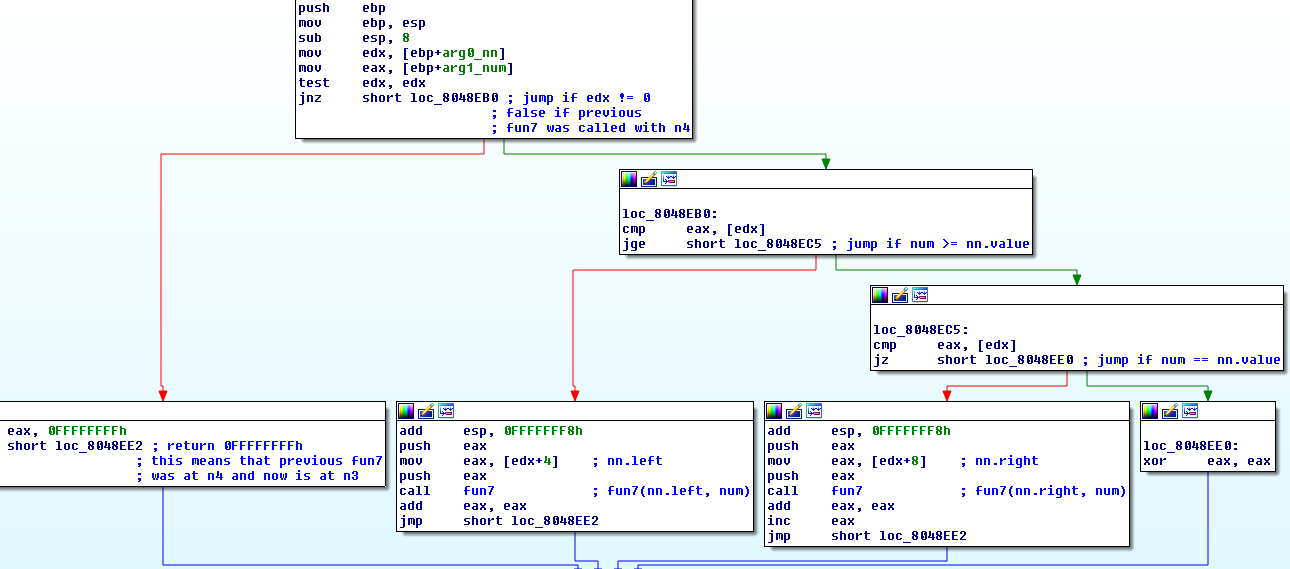
Below is pseudocode of what it does.

if arg0 == 0:
   returns 0x0FFFFFFFF
if our number >= arg0.value:
   if our number == arg0.value:
      returns 0
   result = fun7(arg0.right, our number)    soo it's recursive
   returns 2*result + 1

result = fun7(arg0.left, our number)
returns 2*result 

The function calls itself until it reaches the end of the graph or our number == arg0.value. 4x nodes all have null next addresses and when fun7(arg0.left/right => 0x00000000 , number) is called => arg0 == 0 will be true.

To pass the secret phase we must find such an input that fun7 returns 7. There are two ways to find the right input.

1. Bruteforce it
2. Use logic

At first I solved it with bruteforce using this script:

#!/usr/bin/env python3

class nn:
   def __init__(self,value):
      self.value = value
      self.next_left = None
      self.next_right = None

n01 = nn(0x024)
n21 = nn(0x008)
n22 = nn(0x032)
n31 = nn(0x006)
n32 = nn(0x016)
n33 = nn(0x02d)
n34 = nn(0x06b)
n41 = nn(0x001)
n42 = nn(0x007)
n43 = nn(0x014)
n44 = nn(0x023)
n45 = nn(0x028)
n46 = nn(0x02f)
n47 = nn(0x063)
n48 = nn(0x3e9)

n01.next_left = n21
n01.next_right = n22

n21.next_left = n31
n21.next_right = n32

n22.next_left = n33
n22.next_right = n34

n31.next_left = n41
n31.next_right = n42

n32.next_left = n43
n32.next_right = n44

n33.next_left = n45
n33.next_right = n46

n34.next_left = n47
n34.next_right = n48


def fun7(n, num):
   if n == None:
      return 0x0FFFFFFFF

   if num >= n.value:
      if num == n.value:
         return 0

      result = fun7(n.next_right, num)
      result = 2*result + 1
      return result

   result = fun7(n.next_left, num)
   result = 2*result
   return result

def secret_phase(num):
   if num-1 > 0x3e8:
      #print('Boom! Larger than %d' % (0x3e9))
      return False

   result = fun7(n01, num)
   if result != 7:
      #print('Boom! Not 7')
      return False

   return True

for i in range(0x3e9+1):
   if secret_phase(i):
      print('Key is: ', i)
      input()

$ ./secret_phase.py
Key is:  1001

But you could solve it only by thinking a little and reverse the algorithm. Find the input by knowing the output (7).

• The end result of the first (outermost) fun7 shoud be 7
• 7 is an odd number and the only way to get 7 is at result = 2 x result + 1 part of the code (I’ll call it the odd part, and 2 x result -> the even part)
• That means the result of the second fun7 should be 3 (2*3 +1 = 7)
• To get 3 is only possible again at the odd part
• The result of the third fun7 should be 1 (2*1 +1 = 3 )
• Again, 1 can only be produced in the odd section
• The result of the fourth fun7 should be 0 (2*0 +2 = 1)
• The only possible way fourth fun7 to return 0 is our number to be equal to some of the values of the n4x nodes.
• Also note that all return values (except 0) are odd

Below are the values of all nodes: n01 = 0x024
n21 = 0x008
n22 = 0x032
n31 = 0x006
n32 = 0x016
n33 = 0x02d
n34 = 0x06b
n41 = 0x001
n42 = 0x007
n43 = 0x014
n44 = 0x023
n45 = 0x028
n46 = 0x02f
n47 = 0x063
n48 = 0x3e9

Let’s start again at the first (outermost) fun7 -> fun7(n1, our_num):

• Could our num be equal to n41 = 0x001? No, because n01 (0x24) > n41 and we’ll end up at the even section of the code and couldn’t get an odd number.
• That means every n4x node with value less than 0x24 (n41, n42, n43, n44) is no good
• What about n45 = 0x028 ? No, becase the second fun7 will be called with argument n22=0x32 and everything less will get us to the even section.
• So n45 and n46 are not good.
• n47 = 0x063 ? No, because the third fun7 will have an argument n34 = 0x06b and n47 < n34
• The only answer left is 0x3e9 (1001 in decimal)